

The next step consists in the decomposition of the computational domain Ω into a locally finite number of simplicial cells V i such as tetra- or hexahedra under the premise that all cells have to fit exactly to each other, i.e.
, which contains the space region of interest. The first discretization step of the FI-method consists in the restriction of the electromagnetic field problem, which usually represents an open boundary problem, to a simply connected and bounded space region This mathematical background is corresponding with conformal Edge-Finite-Element schemes used in computational electromagnetics, which are usually rather derived starting from mathematical variational formulations. They closely resemble the discrete formulations of the Finite Integration Technique. In the resulting discrete formulations the equations are typically separated in those which are metric-free, arising from topology, and in those which are metric-depended. Īlgebraic properties of the discrete formulation make it possible to develop long-term stable numerical time integration schemes or accurate eigenvalue solvers avoiding spurious modes. This finite volume-type discretization scheme for Maxwell’s equations is based upon the usage of integral balances and thus allows to prove stability and conservation properties of the discrete fields even before starting with numerical calculations, as described in.
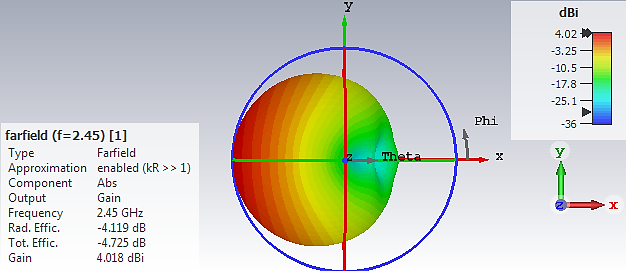
It provides a discrete reformulation of Maxwell’s equations in their integral form suitable for computers and it allows to simulate real-world electromagnetic field problems with complex geometries. The Finite Integration Technique (FIT) was first presented in 1977 by Prof.
#Cst microwave studio far field software
It is also the mathematical base for simulation software MAFIA and CST MICROWAVE STUDIO ®. So FIT is a numerical simulation method for approximation-free solutions of Maxwell's equations in their integral form. In addition, the basic algebraic properties of this discrete electromagnetic field theory allow to analytically and algebraically prove conservation properties with respect to energy and charge of the discrete formulation and gives an explanation of the stability properties of numerical formulations in the time domain. The resulting matrix equations of the discretized fields can be used for efficient numerical simulations. The Finite Integration Technique (FIT) is a consistent discretization scheme for Maxwell’s equations in their integral form. New for February 2015! This page was contributed by Klaus Debes. Click here to go to our main page on Maxwell's Equations


 0 kommentar(er)
0 kommentar(er)
